Image by: Jesus Najera
The mathematical constant, e ,is something that anyone studying science must have come across at some point in their course of study. But what is it? Where did it come from? Let us know and understand.
The credit for discovering this constant actually goes to Jacob Bernoulli. He discovered this constant in 1683 while examining a question related to compound interest. This constant is also known as Euler's constant or Euler's Number for it was Leonhard Euler who first started using the letter e to denote this constant and this representation is now the standard representation, retained in his honor. The constant is also called Napier's Constant for it serves as the base of the natural logarithm. In fact, the constant e is one of the most important mathematical constants along with 0, 1, π, the ratio of a circle's circumference and its diameter and i, the square root of minus one. All these constants are connected by Euler's Identity
which I will talk about in a later blog.
This formula is also considered by Mathematicians as the most beautiful equation in Mathematics.
As stated earlier, Jacob Bernoulli discovered this constant while working on a problem related to compound interest. The following is the problem he was working on:
An account starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2.00. What happens if the interest is computed and credited more frequently during the year?
Looking at this problem now, it may seem simple for we are already familiar with the concept of compound interest and the related formulas, something which is taught as early as grade 8 itself. But still, let us analyze this problem.
Having $1 in hand and the rate of interest being 100%, after 1 year the sum we will have will be,
Sum after 1 year= Original sum + Interest on this sum
Which is simply 1+100% of 1= $2
Now after 1 year we have $2
Let us consider the next year
The sum will be 2+100% or 2 = $4
After 2 years we have $4
In the third year again the sum we will have will be 4+100% of 4 = $8
As you may have very well guessed the trend, the sum is increasing as $1,$2,$4,$8,$16,.......... and so on in multiples of 2. But wait a minute! This is rather discrete. We cannot expect to get the whole of the interest at the end of the year. What happens throughout the year? The sum must have increased gradually and continuously throughout the year.
Let us analyze this.
Let us divide our year into two halves. We get 50% interest in the first half and the remaining 50% in the latter half of the year.
So after the first half, the sum in hand = 1+50% of 1 = $1.5
Now the interest for the latter half will be calculated on this $1.5
So after the second half, the sum in hand= 1.5 + 50% of 1.5 = $2.25
Notice this sum is greater than the sum we obtained on calculating the interest discretely.
Now let us divide our year into four halves(quarters), 25% interest being given in each half such that 100% interest is given throughout the year.
Now
The sum in hand after first quarter = 1+25% of 1 =$1.25
The sum in hand after second quarter= 1.25 + 25% of 1.25 = $1.5625
Again notice that this sum is more than the sum we obtained after half a year in the previous case.
The sum in hand after third quarter= 1.5625+25% of 1.5625 = $1.953125
The sum in hand after the fourth and last quarter= 1.953125+25% of 1.953125=$2.44140625
Again notice this is more than the sum obtained after 1 year in the previous two cases
Let us write these sums down
When year was taken as a whole we received $2 which can be calculated as,
Then we divided the year into two halves and received the amount which can be calculated as,
Then we divided the year into four equal portions and received the amount which can be calculated as,
Do you see the trend?
If we divide our year in n equal portions, the sum we will receive at the end of the year will be,
Now that we have a general formula let us put some more values and analyze what amount we receive at the end of the year.
Put n=20, we get 2.653297705
Put n=50, we get 2.691587029
Put n=100, we get 2.704813829
Put n=150, we get 2.709275911
Put n=200, we get 2.711517123
Put n=300, we get 2.713765158
Put n=365, we get 2.714408711
Notice how we are coming closer and closer to a constant valued 2.718281828
Notice that the value is increasing with increasing with increasing value of n but this increase is getting slower and slower.
Now let us say we divide this 1 year into a large number of portions, so large that it tends to infinity, that is we divide our year into infinite number of portions, what value will we get?
We get our magical number e
Note that e is an irrational number
The digits after the decimal point never terminate.
We took the interest as 100%, now let us take the interest as x, so the amount we get after one year will become,
In fact we can express this constant as infinite summations
Here, we have only confined ourselves to the concept about the discovery of e. This constant also has many other important applications which I will surely talk about in later blogs.
Thanks for reading.
Happy Learning.











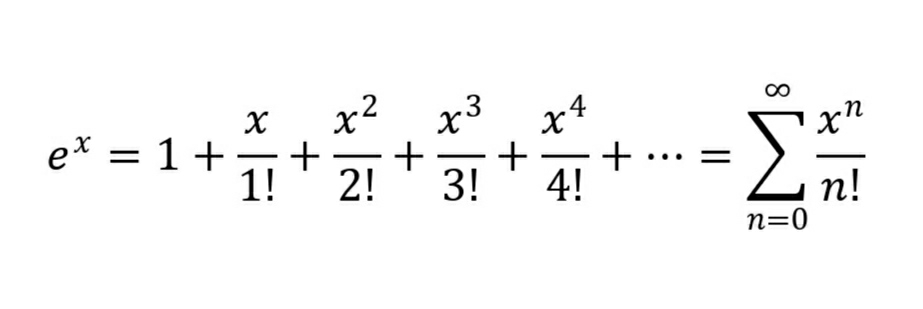


1 Comments
Excellent work👍👌
ReplyDelete