When we talk about Differential Equations, they are of so many types, each having its own method of solution and as we very well know, solutions of differential equations are of great practical importance.
Now, if a differential equation is expressed in the form of
,it is known as Clairaut's Equation, named after the French mathematician, geophysicist and astronomer, Alexis Clairaut.
Any differential equation which can be expressed in the above mentioned form can be solved very easily. Let's take a look at its solution.
First we differentiate the whole equation with respect to x
As you may have noticed, on differentiating the whole equation with respect to x, the term y' cancels out and we are left with
Hence, we can see this equation has two solutions:
The solution which we obtain through equation 1, we call it as the GENERAL SOLUTION. Let us first analyze the general solution and then move on to the solution we obtain through equation 2.
Now the solution of equation 1 implies that y' must be constant as
Let y'=p
Thus, for any equation reducible to the form
The GENERAL SOLUTION is found by simply replacing p with a constant c, that is, the solution simply becomes
How cool is that?
But we are forgetting something. There is also an equation 2 which can be 0. What kind of solution will equation 2 give? Let us know.
Whereas equation 1 gives a family of curves of the form y=cx+f(c), equation 2 will give a SINGULAR SOLUTION, if and only if its value is 0. It is NOT NECESSARY for equation 2 to be 0 as we will see in the examples I will take up in a later blog.
Now what is this singular solution?
If equation 2 is 0, then
The solution thus obtained is known as SINGULAR SOLUTION.
A new question
What does this singular solution represent?
The singular solution solution represents the curve which is the envelope of the family of curves represented by the general solution.
Another question, what is an envelope? Funny how a solution is creating even more problems. A bad math joke. Moving on.....
When we talk about curves, an envelope of a curve represents a curve which is always tangent to a given family of curves. We will learn about this through graph when we solve different equations of this type.
So this was all about the theory of the Clairaut's Equation
Stay tuned for some nice questions where we see how it is applied and the related graphs in a later blog.
Till then,
Thanks for Reading
And
Happy Learning
Update: Part 2 is now up where I solve Clairaut Type differential equations



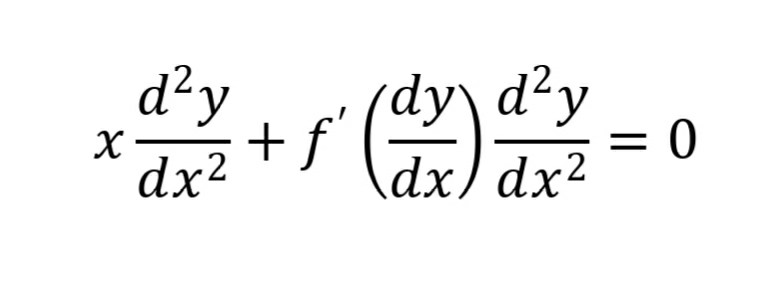











0 Comments